RAICES CUADRADA DE MATRICES

Sea una función y = f(x) y x₀ un punto del eje X. Si se toma un punto x₀ + h muy próximo a x₀ (h es un número infinitamente pequeño), a medida que se hace tender h a cero, la recta secante (en rojo de la figura) que une los puntos

( x₀, f(x₀ ) ) y ( x₀ + h, f(x₀ + h) ), tiende a confundirse con la tangente (en azul de la figura) a la curva en el punto (x₀,f(x₀ )).

que determina la tangente con ese mismo eje, en el triángulo rectángulo de vértices

(x₀,f(x₀ )), (x₀ + h,f(x₀ + h)) y (x₀ + h,f(x₀ )), se verifica:

Al hacer tender h a cero, y puesto que la secante tiende a confundirse con un segmento

de la tangente, es decir, si miras la figura, al hacer que h tienda a cero la línea roja se acerca a la línea azul por lo que:

tg a_h tiende a tg a, es decir,

a la pendiente de la tangente a la curva en el punto (x₀,f(x₀ )).

Esto se expresa matemáticamente así:

 

 

Derivada de una función en un punto Dada una función y = f(x), se llama derivada de la función f en un punto x0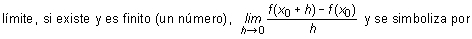

f '(x₀ ) (efe prima de equis sub-cero) o por D(f(x0 )):

 

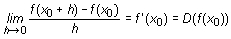Cuando este límite existe (y es finito) se dice que la función f(x) es derivable en el punto x₀.

 

 

Significado de la derivada

Puesto que

 

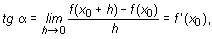la derivada de la función en un punto x₀ no es otra cosa que la pendiente de la tangente a la curva (gráfica de la función) en (x₀, f(x₀ )).

 

 

http://www.decarcaixent.com/actividades/mates/derivadas/derivadas2.htm